Frequency Ratios in Intervals: Math and Music


When humans first started making music, we most likely didn’t think very mathematically about the sounds we were making. Instruments were probably made to play notes that sounded good together, and we created some pretty beautiful music even with that.
Now, it has become obvious that the more understanding of how notes relate can help us make even better music. This mathematical understanding of music started with a guy name Pythagoras (yep, he’s the guy with the theorem). For the most part, we seem to only discuss him when trying to find lengths of the sides of right triangles, but his work was useful in many other applications as well.
He discovered that strings that had a 1:2 ratio would be an octave apart. So, for example, if I had 2 strings, one string exactly double the length of the other, when I plucked those two strings, I would get notes exactly one octave apart.
To understand how exactly why this happens and how it relates to intervals, we have to delve into how sound waves work. You can read a past blog post on it here:
The frequency, or the number of waves that travel in a fixed amount of time, determine the pitch of a sound. It is measured in a unit called Hertz (Hz). A higher frequency will mean a higher pitched sound, and a lower frequency will mean a lower pitched sound.
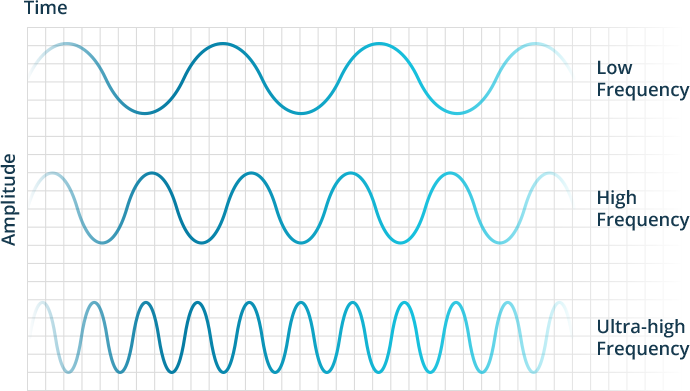

When a string is pulled, it creates sound waves at a certain frequency. A string that is 1/2 the length of another creates a wave that is 1/2 the frequency of the other. In other words, the note that is one octave above the other has sound waves that vibrate at exactly twice the speed of the other.
Just like Pythagoras did, musicians, mathematicians, and scientists started to look at ratios of other frequencies to find relationships in how certain notes sounded together.
In music theory today, the intervals of a 4th, 5th, and 8ve (octave) are classified as perfect intervals. They are called this because they created the greatest degree of sensory consonance; in basic terms, they sounded good. But as more findings arose, we noticed that there was a reason for that.
People already knew that two notes that had a frequency in the ratio of 1:2 would create the interval of an octave. So, the note A4 (440 Hz) had an obvious relationship with the note exactly an octave above it, A5 (880 Hz). As one can tell, A5 is vibrating at exactly double the speed of the note A4.
To get a perfect fifth, they realized, they needed to reach a 2:3 ratio of frequency. And to get a fourth? A 3:4 ratio.
This is how our perfect intervals sound:
Had they discovered something?
It was found that notes that sounded “harmonious” together had certain ratios in frequency. Ratios that were simple, like 1:2, 2:3, or 3:4 sounded much more natural than others, and we liked them more.
But what do the more dissonant intervals have in common? As the ratio started became more complicated; 5:8 to 16:9 to 16:15, the intervals started sounding more unnatural.
Let’s go down our list of intervals to see how this works.
We can start with the major third. The notes that are part of this interval have a frequency with the ratio 4:5. When we listen to it, we can tell that it sounds fairly natural and harmonius.
We can then continue down the list of intervals in terms of ratio. Let’s go to the minor third.
Then, we can continue to the major second, with the ratio of 9:8.
Lastly, we have the minor second. The ratio between notes in this interval have the ratio of 16:15.
Can you see the pattern here? As the ratio between notes becomes more and more complicated, the dissonance is much higher. In a future post, we’ll discuss some other hidden patterns that we might not have discussed.
In the meantime, take some time to really appreciate the hidden science behind the music we listen to. Musical geniuses like Bach and Mozart used these exact mathematical ideas to write their music, whether they did it unconsciously or knowingly. When we play harmonics on a string instrument, we’re literally dividing our strings in half to play an octave above what our string is supposed to sound like.
Resources:
- “Musical Scales.” Musical Scales and Intervals, hyperphysics.phy-astr.gsu.edu/hbase/Music/mussca.html.
- McDermott, Josh H, et al. “Musical Intervals and Relative Pitch: Frequency Resolution, Not Interval Resolution, Is Special.” The Journal of the Acoustical Society of America, Acoustical Society of America, Oct. 2010, www.ncbi.nlm.nih.gov/pmc/articles/PMC2981111/.

